Fast computation of reconciled forecasts for hierarchical and grouped time series

Abstract

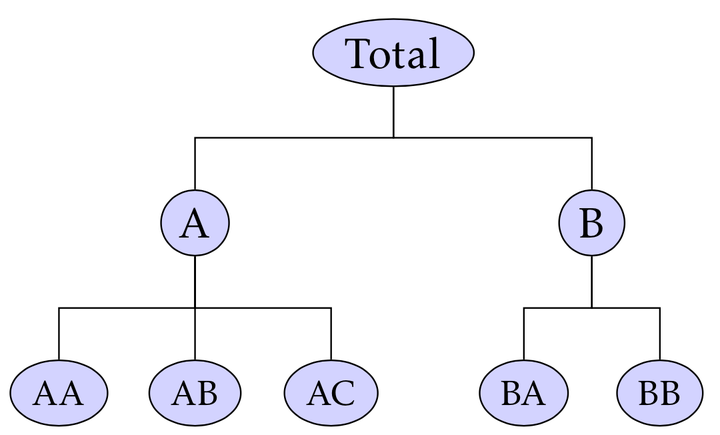
It is shown that the least squares approach to reconciling hierarchical time series forecasts can be extended to much more general collections of time series with aggregation constraints. The constraints arise due to the need for forecasts of collections of time series to add up in the same way as the observed time series. It is also shown that the computations involved can be handled efficiently by exploiting the structure of the associated design matrix, or by using sparse matrix routines. The proposed algorithms make forecast reconciliation feasible in business applications involving very large numbers of time series.